上次說到有時候我們會從觀察到的現象去猜導致這個現象的函數(原因)
我們首先會先從最簡單的函數開始
也就是多項式函數
但是為什麼我們一開始不會選擇太高次的多項式呢？

舉個例子，假設真實現象是由 所導致

# 假設目標函數
def target(x):
    return x**2+1

但是現實觀察中總會免不了有誤差
假設每次誤差都不超過真實值的 0.2

# 誤差的分配
mu, sigma = 0, 0.2

最後創造觀察集

import random
import numpy as np

# 產生樣本集
sample_x = np.arange(-5, 5, 0.5)
sample_y = [target(x) + np.random.normal(mu, sigma)*target(x) for x in sample_x]

畫出觀察集的樣子

import matplotlib.pyplot as plt
x_list = np.arange(-5, 5, 0.1)

# 畫出觀察集
fig = plt.figure(figsize = (6,6))
plt.plot(x_list, target(x_list), color = 'red', label = 'target')
plt.scatter(sample_x, sample_y, s = 50)
plt.legend()
plt.show()

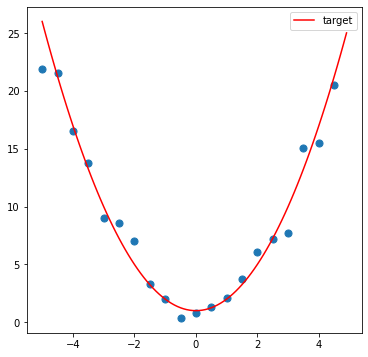
如果我們不考慮誤差
直接使用靈活的高次多項式盡可能的穿過觀察點
(圖中為 Lagrange 插值多項式，理論上必能通過所有觀察點，但可能因精度影響無法呈現)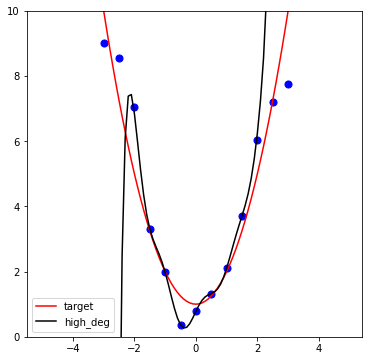

但是這種函數的行為就像是看著下一個目標前進
所以才能完美的通過所有觀察點
而我們想猜導致觀察現象的函數的主要目標是預測未來
對於還沒發生的未來，根本沒有下一個目標
所以高次多項式函數就不會是我們的首選

RN：多項式函數是一種最簡單的函數
　　而且增加最高次項就可以使函數圖形變的更加靈活
　　強迫它通過觀察點或從觀察點旁經過
　　但是過度增加項數，會失去對預測未來的彈性
　　這樣的舉例有比較清楚嗎(´ΘωΘ`)？

75：zzz...(¦3[▓▓]

RN：...算了，去吃牛肉麵好了...